Probability: Complements, Intersections, Unions, Conditional

Objectives

1. To learn how some events are naturally expressible in terms of other events.
2. To learn how to use special formulas for the probability of an event that is expressed in terms of one or more other events.

Probability Rule for Complements

P(A^c)=1−P(A)

The complement of an event A in a sample space S, denoted A^c, is the collection of all outcomes in S that are not elements of the set A. It corresponds to negating any description in words of the event A.

Intersection of Events

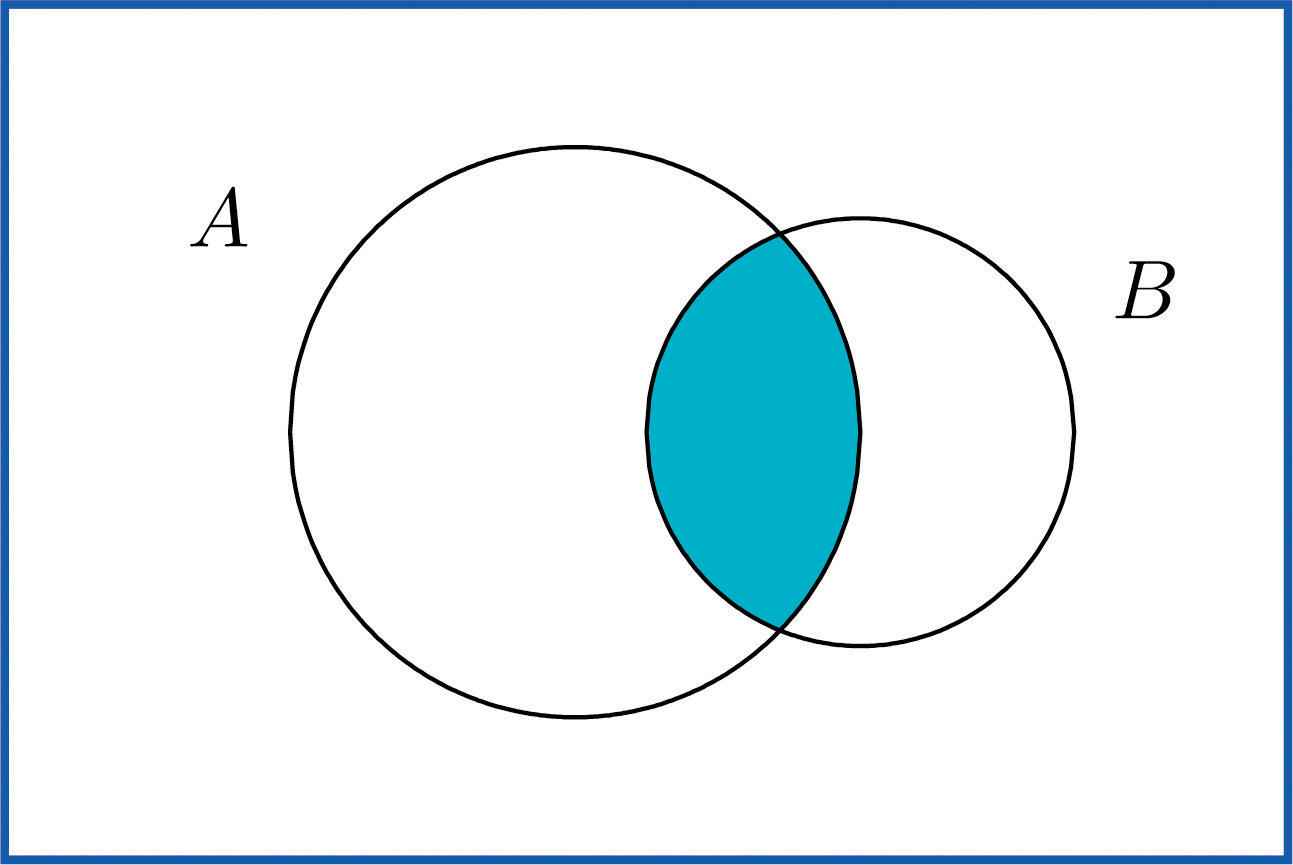
The intersection of events A and B, denoted A ∩ B, is the collection of all outcomes that are elements of both of the sets A and B. It corresponds to combining descriptions of the two events using the word “and.”

Mutually Exclusive Events

Events A and B are mutually exclusive if they have no elements in common.

Events A and B are mutually exclusive if and only if

P(A∩B)=0

• Any event A and its complement A^c are mutually exclusive
• but A and B can be mutually exclusive without being complements.

Union of Events

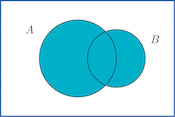
The union of events A and B, denoted A ∪ B, is the collection of all outcomes that are elements of one or the other of the sets A and B, or of both of them. It corresponds to combining descriptions of the two events using the word “or.”

Additive Rule of Probability

// Probability(union of A & B)
P(A∪B) = P(A) + /* all of A */
         P(B) - /* all of B */
         P(A∩B) /* less the intersection of A & B */

Conditional Probability

In general, the revised probability that an event A has occurred, taking into account the additional information that another event B has definitely occurred on this trial of the experiment, is called the conditional probability of A given B and is denoted by P(A|B)

//
// the conditional probability of A given B
// 
// ex. A = odds of rolling a 5 (1/6)
//     B = an odd number has been rolled (3/6)
//
P(A|B)

The conditional probability of A given B, denoted P(A|B), is the probability that event A has occurred in a trial of a random experiment for which it is known that event B has definitely occurred. It may be computed by means of the following formula:

P(A|B)= P(A∩B) / /* intersecton of A & B */
        P(B)     /* divide by the probability of B */

// 
// A = rolling a 5, (5)
// B = rolling an odd (1, 3, 5)
//
// P(A|B) = what are the odds of rolling a 5 given rolling an odd?
// 
// P(A∩B) = (5) ∩ (1, 3, 5) = (5), p(5) = P(A∩B) = 1/6
// P(B) = (1, 3, 5) = 3/6
// 
// P(A|B) = P(A∩B) 1/6 / 
//          P(B)   1/2
//
// -> 1/3
//

Independent Events

Events A and B are independent if

P(A∩B)= P(A)·P(B)

//
// A single fair die is rolled.
// Let A={3} and B={1,3,5}. Are A and B independent?
//
// P(A)=1∕6, P(B)=1∕2
//
// P(A∩B)=P({3})=1∕6
//
// P(A)·P(B)=(1∕6)(1∕2)=1∕12
//
// P(A∩B) != P(A)·P(B)
// 1/6    != 1/12
//
// -> not independent
//

The concept of independence applies to any number of events. For example, three events A, B, and C are independent if P(A∩B∩C)=P(A)·P(B)·P(C).

Probabilities on Tree Diagrams

Some probability problems are made much simpler when approached using a tree diagram. The next example illustrates how to place probabilities on a tree diagram and use it to solve a problem.